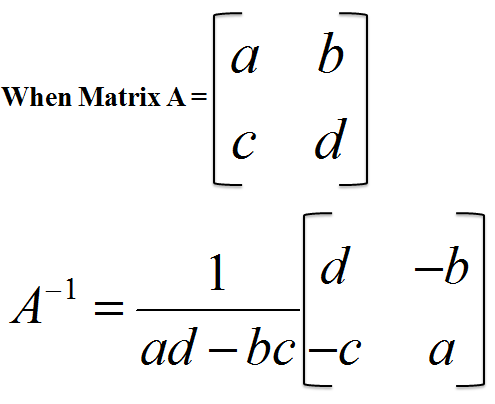Difference between Adjoint and Inverse
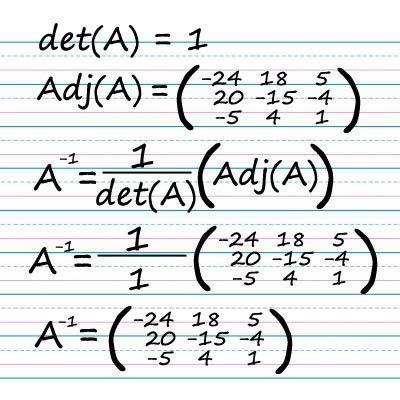
Students of mathematics, algebra, statistics and probability must learn and understand the differences between adjoint matrix and inverse matrix to be able to solve complex problems or equations. It should be noted that inverse and adjoint matrices are used in linear operations in a matrix.
These two types of matrices have different properties and their use is also significantly different, albeit inter connected. Adjoint matrix is basically essential in calculating the inverse matrix of any given square matrix. Inverse matrix on the other hand, can only be calculated if the determinant of any matrix is not less than or equal to zero.
Multiplying the inverse of a matrix with it will result in an identity matrix, but this is not the case in adjoint matrix.
Furthermore, derivation of a determinant using the Jacobs formula also depends on adjoint matrices. The adjoint matrix has commonly been used in mathematics since decades but now it is mostly used for complex conjugate of matrices. Therefore, it is advised to use the terms adjugate matrix rather than using adjoint matrix.
A matrix satisfying the condition |A| = det(A) ≠ 0 can be termed as an inverse, non degenerative and non singular matrix. Furthermore, a square matrix and its inverse always has the same size.
In the equation given below C is the adjoint matrix of the cofactor matrix A:
C = adj(A)
Note that the cofactor matrix is defined as C = (-1)i+j Mij where Mij is the minor of the ijth item. Removing the jth and ith element from the column results in the determinant of the matrix to be directly obtained. It is recommended to determine the minors of each element and work out the transpose of the cofactor matrix to be able to compute the adjugate matrix accurately.
Instructions
-
1
Adjoint
The transpose of the cofactor matrix is known as the adjugate or adjoint matrix.
Adjoint matrix has numerous applications in the field of mathematics, sciences, statistics and probability.
Image courtesy: earthnote.blogspot.com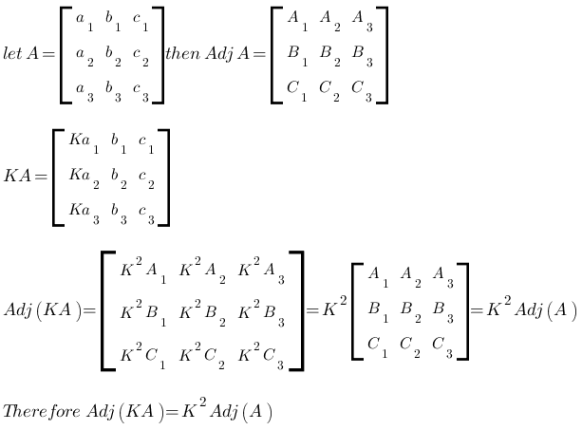
-
2
Inverse
Inverse of a matrix can be computed only if the determinant of any matrix A is not less than or equal to zero. When multiplication of two or more matrices is performed and then matrix is the identity matrix, the phenomenon is called the inverse of a matrix. Therefore, if AB = BA = I, then B is the inverse matrix of A and A is the inverse of matrix B.
Image courtesy: amazon.com
 ≠ 0 can be termed as an inverse, non degenerative and non singular matrix. Furthermore, a square matrix and its inverse always has the same size.
In the equation given below C is the adjoint matrix of the cofactor matrix A:
C = adj(A)
Note that the cofactor matrix is defined as C = (-1)i+j Mij where Mij is the minor of the ijth item. Removing the jth and ith element from the column results in the determinant of the matrix to be directly obtained. It is recommended to determine the minors of each element and work out the transpose of the cofactor matrix to be able to compute the adjugate matrix accurately.
Next%20stop%3A%20Pinterest "Pin It")
