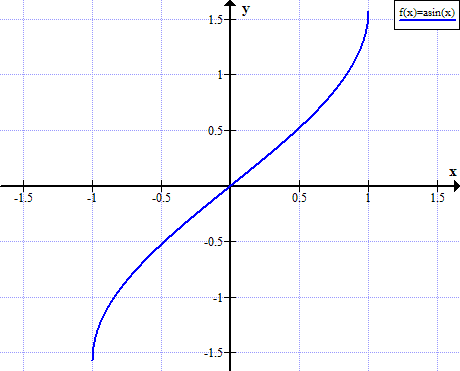
Difference between Sine and Arcsine
There is a significant difference between sine and sine inverse, which is also known as arcsine. They are both basic ratios of trigonometry, and you will encounter them in almost every mathematical coursework you take after high school. Sine helps you calculate the value of an angle if the different sides of a triangle are given. However, in case you want to calculate the sides and you are provided with an angle, you will have to use arcsine.
There are two major differences between sine and arcsine:
The basic trigonometric function is sine, and arcsine is its inverse.
Secondly, the sine function will calculate a number or an angle in radians and between the range of -1 and +1. On the other hand, an arcsine will give the value in terms of a real number and within the range of -1, +1 to -π, +π.
Instructions
-
1
Sine
The perfect way to define sine is through a right angled triangle. In the most basic form, sine is a ratio between the perpendicular and the hypotenuse. So basically, sin α = perpendicular/hypotenuse, with α being the angle between these two lines.
Sine can also be defined as a function of an angle, but the magnitude is always given in radians. In modern day mathematics, it is known as a solution to certain differential equations. The function, in real numbers, will range between negative infinity to positive infinity.
Image Courtesy: conservapedia.com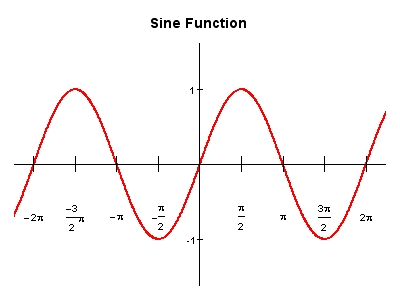
-
2
Arsine (or Sine inverse)
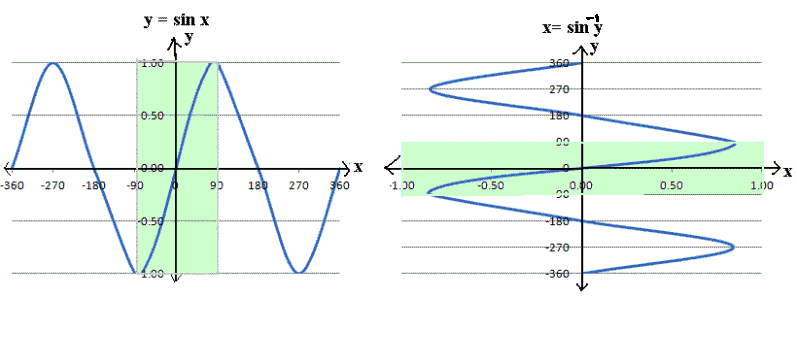
The inverse of sine is an arcsine. This function is used to calculate the angle between any two sides which are given in terms of real numbers. The domain and the co-domain in this case is the opposite of a sine function, and shaped backwards. It definitely relates to the sine function as the co-domain of a sine function is the domain of the arcsine function and vice versa. Mostly, the real numbers are mapped between the range of -1, +1 to R.
The single problem with this inverse function is in its validity. Mostly, the inverse function is not valid when the whole domain is selected from the original function. Basically, there is a violation in the definition of the function itself. This is the reason why the range of an inverse function of sine is restricted to -π, +π. This way, the different elements in a single domain do not get mixed with the elements included in the co-domain. Hence, when 1 is subtracted from sine, the range is from -1, +1 to -π, +π.
Image Courtesy: rapidtables.com