Finding the Volume of a Solid Surface

In early classes, students are taught that the volume of a substance is actually the space that it occupies. Unlike area, which involves the length and breadth for measurement, volume also involves the height as it is a three dimensional quantity. Although it is quite easy to find and determine the volume of almost every shape or solid, but when it comes to preparing for an exam, some students tend to feel a bit overwhelmed with this topic. This topic, which deals with finding the volume and surface area, is included in Mensuration – a branch of mathematics that deals with the study of Geometric shapes along with finding their areas, volumes and different parameters.
Instructions
-
1
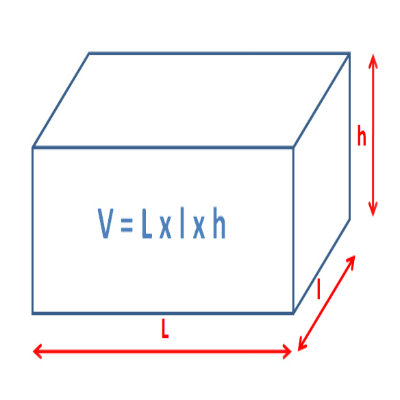
Volume of a Rectangle or a Parallelogram
Finding volume of a rectangle or parallelogram is quite easy as it is simply the product of base area and the height. In other words, you simply put values in the below given formula.
Volume = Length x Breadth x Height
Sometimes you will be provided with the volume and base area and you will have to calculate the height. On the other hand, at times you will be given the volume and you will have to find the length of three sides. Consider the following two example:
Example 1. Find the height of the rectangular block that has a base area of 30 sq m and volume of 120 cubic meters.
Volume = Length x Breadth x Height
Base Area = Length x Breadth
Given that:
Volume = 120 cubic meters
Base Area = 30 sq m
Height = Volume/ Base Area
= 120/30
= 4 m
Example 2. Find the length of sides of a cube whose volume is 125 cubic centimeters.
Volume of a Cube = Length x Breath x Height
For a cube, Length = Breadth = Height
So, Volume of Cube = L x L x L
125 = L3
L = 3√125
L = 5 cm
-
2
Volume of a Cuboid
Finding the volume of a cuboid is almost as easy as finding the volume of a rectangle. However, you can be given a situation that may prove to be confusing. Make sure you know the basics of finding volume while making calculations.
Example. A rectangular reservoir contained about 2.7 liters of water. To avoid overflow, the water was transferred into a bigger rectangular box having base area of 900 square centimeter and volume of 3600 cubic centimeters. Find the height of water level in the new tank.
Volume of Water = 2.7 liters = 2700 cubic centimeters
Base Area = 900 sq cm
Since Volume = Base Area x Height
So Height = Volume / Base Area
= 2700 / 900
= 3 cm
-
3
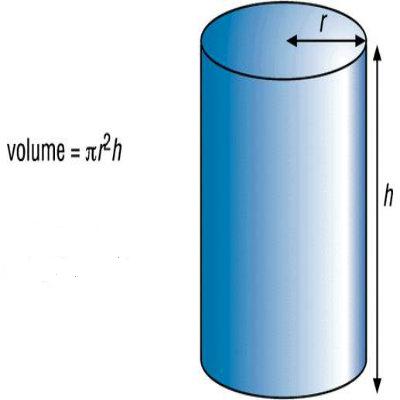
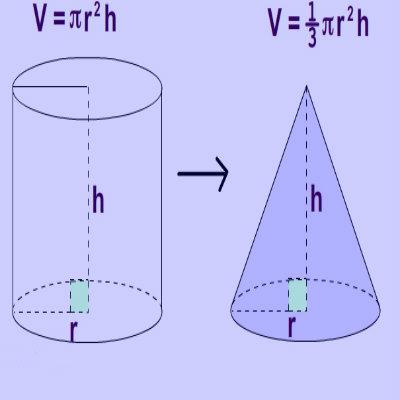
Volume of Cylinder
If you know how to find the area of a circle, then finding the volume of a cylinder is very easy. Considering that a cylinder has a circular base so its volume is calculated by multiplying the area of its circular base with the height. Hence,
Volume of Cylinder = π r2h
Example. A cylinder is twice as long as it is thick. If the diameter of the cylinder is 14 cm then calculate the volume.
Diameter = 14cm Radius = 7cm
Height = 2 (Diameter)
= 2(14)
= 28 cm
Volume = π r2h
= 22/7 (7)2(14)
= 2156 cm3
-
4
Volume of a Cone
If we look at the shape of a cone, it has some similarities with the cylinder. It has the same circular base and height but occupies lesser space. The volume of a cone is calculated with the below given formula.
Volume of Cone = 1/3 π r2h
Example. Find the volume of a cone that has a slant height of 10 cm and diameter of the base as 8 cm.
Slant height = S = 10
Diameter = D = 8
Radius = r = 4
Height = h =?
By Pythagoras’s Theorem:
Height = √ (10) 2 – (4) 2
= √100 – 16
= √84
= 9.165
Volume = 1/3 π r2h
= 1/3 π (4)2(9.165)
= 1075. 36 cm3
-
5
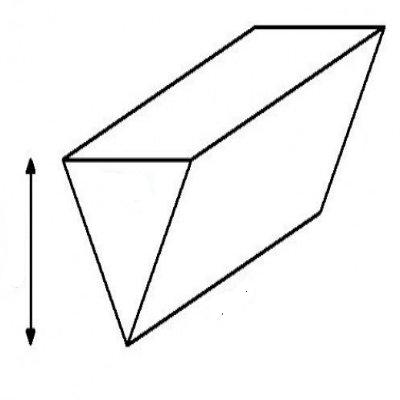
Volume of Prism
The volume of prism is calculated by simply putting values in the below given formula:
Volume of Prism = ½ x length x Width x Height
Example. Water is poured inside a trough having shape of a triangular prism. Considering that the water exactly fills the trough, calculate the height of water when the volume is 300 cm3, length 30 cm and width 10 cm.
Volume of Prism trough = 300
Length = 30
Width = 10
Height =?
Volume = ½ x length x Width x Height
300 = ½ x 30 x 10 x H
H = 300 / 150
H = 2 cm
-
6
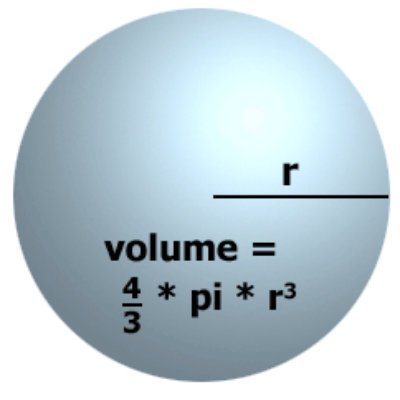
Volume of Sphere
Finding the volume of a sphere is easy. All that you have to do is put the values in the formula given below.
Volume of Sphere = 4/3 π r3
Volume of Hemi-Sphere = ½ x 4/3 π r3
-
7
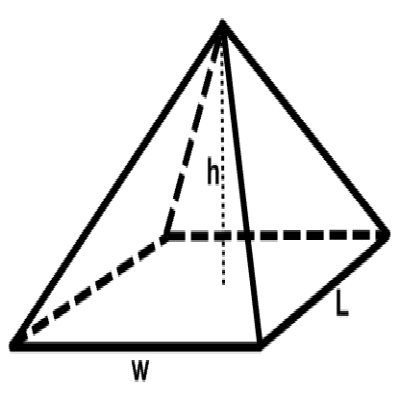
Volume of Pyramid
If you closely observe the shape of a pyramid, it is about one third of a square or cube. Hence the volume of a pyramid can be calculated with the below given formula.
Volume of Pyramid = 1/3 x Base Area x Height
Volume of Pyramid = 1/3 π r2 h