How to Find Surface Area of Solids

When we talk about solids, it means things that have a definite volume and a certain shape. From a mathematical perspective, solids are shapes such as rectangle, cuboid, cylinder, cone, prism, sphere, and pyramid. Students start learning about these shapes from elementary level and by the time they reach higher level in their academics, they have to handle certain problems related to these shapes. One of the problems they have to handle involves finding surface area of the above listed shapes. As far as finding the area is concerned, that is easy to find and it can be derived by multiplying the length of the rectangular object with the breadth. However, if there is a question of finding the surface area, then many students are at sea. This article will guide students about finding surface area of different shapes.
Instructions
-
1
Surface Area of a Rectangle or rectangular block
If we consider a rectangular block, it can be observed that there are 6 sides out of which there are 3 pairs of 2 equal and opposite sides. Hence, if we are to find the surface area of the rectangular block or solid, we may first find area of the six sides one by one by multiplying length with breadth. After that we add up the six areas and the sum of all areas will be the total surface area of the solid. However, there is a very easy way to find the surface area.
Example. Find the surface area of a rectangular solid that has length 5m, breadth 4m and height 3m.
Surface Area of Rectangular Block = 2B + Ph
Where:
B = Area of Base or Base Area
P = Perimeter of the Base
h = Height
Hence,
Perimeter = 4 + 4 + 5 + 5 = 18 (adding all sides)
Base Area = 4 x 5 = 20
Putting values in 2B + Ph we get:
2(20) + 18(3)
40 + 54 = 94 Sq meters
-
2
Surface area of a Cuboid
The total surface area of a cuboid is sum of areas of all six faces and is calculated by a simple formula which is 2(lw + wh + hl), where l is the length, w is the width and h is height of the cuboid.
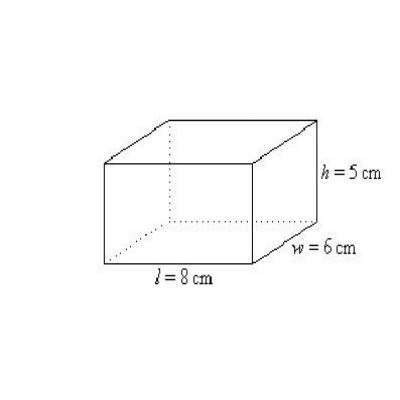
Example. Find the total surface area of a cuboid having length 8cm, width 6cm and height 5cm.
Total Surface Area = 2(l w + w h + h l)
= 2(8 x 6 + 6 x 5 + 5 x 8)
= 2(118)
= 236 Sq. cm
-
3
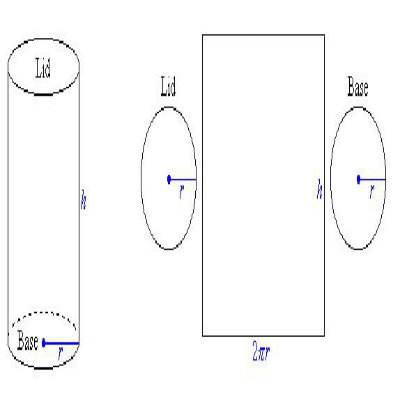
Surface Area of Cylinder
If we look at the shape of a cylinder, it consists of two circular sides and a rectangle that seems to have been folded. Hence, the surface area of rectangle can be found by the following formula:
Surface area = 2 π r (r + h)
Where:
π is Pi, approximately 3.142
r is the radius of the cylinder
h is height of the cylinder
Example. Find surface area of cylinder with height 10cm and diameter 4 cm.
Diameter = Twice the Radius
Radius = Diameter/ 2
R = D/2 = 4/2 = 2cm
Now putting values in formula 2 π r (r + h) we get:
Surface Area = 2 π (2) (2 + 10)
= 4 π (12)
= 48 π
= 150.816 sq.cm
-
4
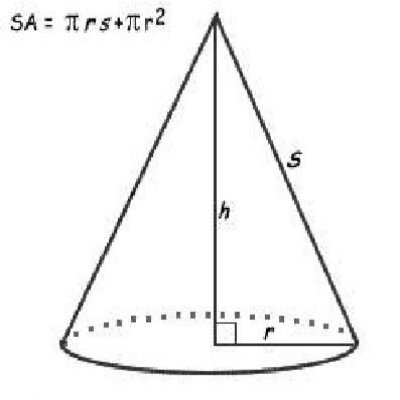
Surface Area of Cone
It is very easy to find the surface area of a cone. We just need to know two things such as the slant height, and the radius of the base of the cone.
Surface Area = π r s + π r2 (Where r is radius of the base and s is the slant height)
Example. Find Surface Area of the cone with radius 4 cm and slant height 10 cm.
Putting values in π r s + π r2 we get:
Surface Area = π (4) (10) + π (4)2
= π (40 + 16)
= π (56)
= 175.952 sq.cm
-
5
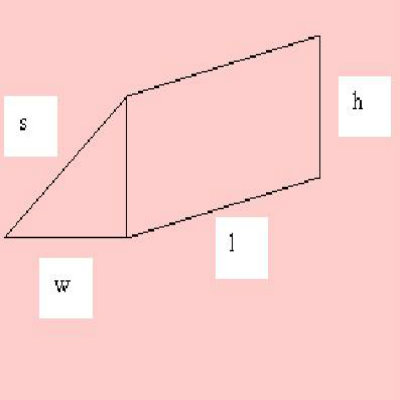
Surface Area of Prism
When we talk about prisms, they are generally of three types; rectangular, cylindrical and triangular. Finding the surface area of rectangular and cylindrical prism is very much similar to finding the area of a cuboid and cylinder, but for a triangular prism it is different. The below given formula is used to find the area of triangular prism.
Base shape: Triangle: base 'b', height 'h', and sides S1, S2 and S3
Area of base: ½ x base × height
Perimeter of base: S1+ S2 + S3
Surface area = b h + (S1+ S2 + S3) h
Where:
S1, S2 and S3 are lengths of the sides of the base
h is the height
b is the base area
If it is a right triangular prism then the formula is:
SA = wh + lw + lh + ls (reference to the provided Image)
-
6
Surface Area of Sphere
It is very simple to find the surface area of a sphere or hemi-sphere by the below given formula.
Surface Area of Sphere = 4 π r2
Surface Are of Hemi-Sphere = ½ x 4 π r2

-
7
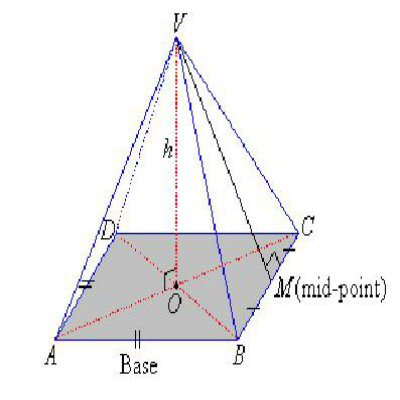
Surface Area of Pyramid
When we talk about a Pyramid, it is generally a three-dimensional figure with a rectangular base and four triangular faces. All the triangular faces meet at a point called vertex or apex of the pyramid. It may be long but not difficult to find the surface area of a pyramid. You can either add areas of four triangles and one square to find the surface area of a pyramid, or simply use the below given formula:
Surface Area = 2 B S + B2
Where:
B is the length of square base
S is the slant height which is normally given or can be calculated by Pythagoras’s Theorem with perpendicular height known.