How to Solve Quadratic Equations
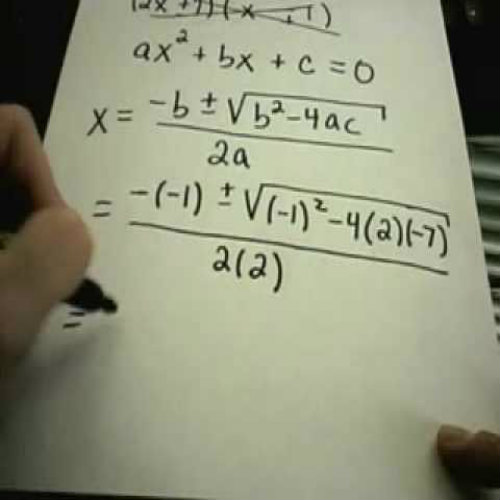
In some mathematical equations we have to calculate two different values of a single variable. Such equations are called Quadratic Equations and it is generally represented in the form ax ² + bx + c (where a ≠ 0). In the equation we can see that the ‘x’ is a variable and a, b and c are constants. As the variable ‘x’ has power ‘2’ so this is another reason for having two values of ‘x’. There are quite a few methods for solving quadratic equations and some of the very common used in schools include factorization method, completing square method, graphical method and by quadratic formula. If you have any problem in solving quadratic equations then the next few minutes will make you change your thoughts.
Instructions
-
1
The Factorization Method
Consider the equation x ² - 7x + 12 = 0
The above equation is formed by multiplying two factors or linear equations. Solving the above equation, we simply break the equation into the two original linear equations and get the two values of ‘x’. Given below is the way we do it:
x ² - 7x + 12 = 0
Multiply coefficient of x2 with the constant 12. The answer will ofcourse be 12. Now come up with those two factors of number 12 which give you ‘-7’ when added or subtracted. Upon calculating you will get:
x ² - 3x – 4x + 12 = 0 ( adding 3 and 4 gives you 7)
x (x – 3) – 4 (x – 3) = 0 ( x – 3 is a common factor)
(x – 3) (x – 4) = 0
Either x – 3 = 0
Or x – 4 = 0
Solving we get:
X = 3 and X = 4 -
2
Completing Square Method
This method involves the concept of the following algebraic formulas:
(a+ b)² = a2 + 2ab + b2
(a - b)² = a2 - 2ab + b2
a² - b² = (a + b) (a – b)
For a quadratic equation of the form x² + 8x + 16, instead of going for factors we see whether the equation can be converted or broken down into any of the above three perfect squares. Solving we get:
x² + 8x + (4)² = 0
x² + 2(1)(4) + (4)² = 0
The above equation can be written as:
x² + 2(1)(4) + (4)² = (x + 4)²
Hence the above equation satisfies the formula (a+ b)² = a² + 2ab + b² . This is how we solve a Quadratic Equation according to Perfect Square Method. -
3
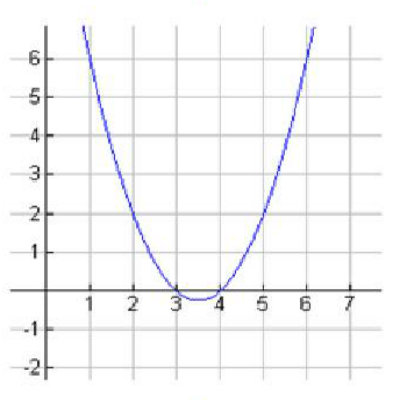
The Graphical Method
Consider the quadratic equation x² - 7x + 12 = 0. When we are to solve the same equation using graphs then it is written as:
Y = x² - 7x + 12
Keeping the above equation we plot a table of values taking values for x of our own choice.
X 0 1 2 3 4 5
Y 12 6 2 0 0 2
As we will plot a graph taking 1cm to represent 1 unit both on x and y-axis, we will have a curve that will intersect the x-axis at x = 3 and x = 4. These two values will be the solution of our quadratic equation. Besides, another indication is that for both the values the value of y is zero.
-
4
The Quadratic Formula
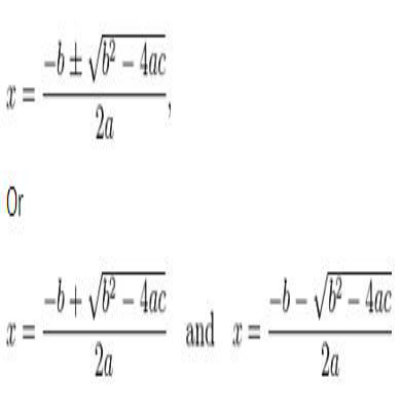
Sometimes when we do not find 2 separate values of a variable applying any of the above methods then we use another technique which is known as the quadratic formula. It is a simple formula which is represented in the image on the right.
Before applying formula we have to ensure that the value of √b² - 4ac is not negative. Once we are sure it is not negative then by solving the quadratic formula we can find the two different values of ‘X’.
. In the equation we can see that the ‘x’ is a variable and a, b and c are constants. As the variable ‘x’ has power ‘2’ so this is another reason for having two values of ‘x’. There are quite a few methods for solving quadratic equations and some of the very common used in schools include factorization method, completing square method, graphical method and by quadratic formula. If you have any problem in solving quadratic equations then the next few minutes will make you change your thoughts.Next%20stop%3A%20Pinterest "Pin It")
