Difference between Arithmetic and Geometric Series
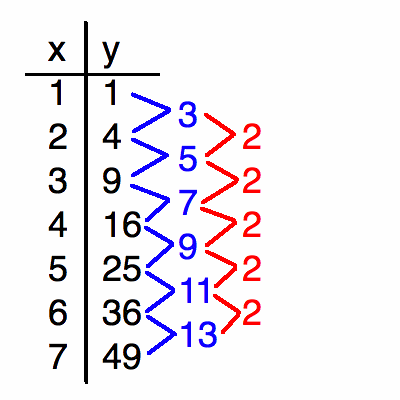
While arithmetic and geometric series have numerous similarities, there are also some key differences between them. You will be required to pay attention to details when working with arithmetic and geometric series. In mathematics, the definition for both series and sequence is identical.
A sequence is a set of number that can be either infinite or finite set. An arithmetic progression is defined as the sequence of numbers where difference between two elements is a constant. A geometric progression on the other hand is the series of constant quotient of two consecutive numbers.
If the series is finite then the number of terms can be counted fairly comfortably. Adding the elements in a progression can be termed as a series. Adding arithmetic progression gives rise to an arithmetic series where the sum of geometric progression is named as geometric series. It is recommended to learn the basics of mathematics and algebra before solving arithmetic and geometric series.
Instructions
-
1
Arithmetic series
An arithmetic series consists of consecutive numbers with the difference being a constant. If this is true then the relationship given below is valid:
Sn = a1 + a2 + a3 + a4 +⋯+ an = ∑ni=1 ai ; where a2 = a1 + d, a3 = a2 + d, and so on.
In the equation above, a1 is the first term, d if the constant difference
The nth term is given by the equation an = a1+ (n-1)d
It should be noted that the behaviour of the series largely depends on the common difference. An increase or decrease in the common difference can make the progression either negative infinite or positive infinite. The formula given below is commonly used to calculate the sum of the series. This formula was developed by famous mathematician and astronomer Aryabhata.
Sn = n/2 (a1+ an ) = n/2 [2a1 + (n-1)d]
Where the Sum Sn can be either finite or infinite depending on the numbers involved in the set and the common difference.
- Image courtesy: verjinschi.disted.camosun.bc.ca
-
2
Geometric series
For a geometric series, the quotient of the consecutive number must be a constant value. According to research conducted by scientists and mathematicians, geometric series can play a key role in solving a variety of engineering problems, especially due to the properties it possesses.
Sn = ar + ar2 + ar3 +⋯+ arn = ∑ni=1 ari
The sum of this type of series can be obtained by using the formula given below:
Sn = a(1-rn) / (1-r)
Where r is the ratio
- Image courtesy: astronomy.mnstate.edu