Difference between Probability Distribution Function and Density Function
Most often, students of statistics are confused with the concepts of probability distribution and probability density function. This article will focus on describing the difference between the two in detail.
Probability distribution function and probability density function are defined over the sample space, in order to assign the appropriate probability value to each part. The major difference is that the probability distribution functions are described for the discrete random variables while probability density functions are defined for the continuous random variables.
Another difference between the two is that in probability distribution function the values can be represented in a table, but that is not possible for the probability density function as the variable is continuous. Also the graphical representation of probability distribution function is through bars and that of probability density function is through curves.
Another significant difference is that in graphical form the height/length of the bars of the probability distribution function must add to 1 while the area under the curve of the probability density function should add to 1.
Instructions
-
1
Probability Distribution Function:
Probability distribution function is defined for discrete random variables. It is a function that allocates the probability values for each event. It provides a relation to the probabilities for the values that the random variable may possess.
- Image Courtesy: theriac.org

-
2
Probability Density Function
Probability density function is the probability distribution function for the continuous random variables. It gives the likelihood of a certain random variable to assume a certain value.
Let X is a discrete random variable,
So the function given as f(x) = P(X = x) for each x that lies within the range of X is called the probability distribution function. A function can serve as the probability distribution function if and only if the function satisfies the following conditions.
1. f(x) ≥ 0
2. ∑ f(x) = 1
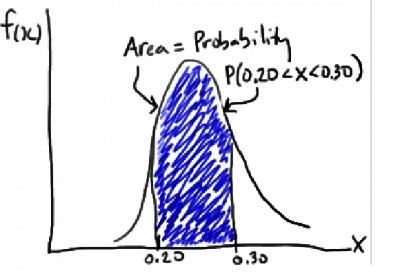
A function f(x) that is defined over the set of real numbers is called the probability density function of the continuous random variable X, if and only if,
P(a ≤ x ≤ b) = a∫b f(x) dx for any real constants a and b.
The probability density function should satisfy the following conditions too.
1. f(x) ≥ 0 for all x: -∞ < x < +∞
2. -∞∫+∞ f(x) dx = 1
- Image Courtesy: onlinecourses.science.psu.edu