Difference Between Transpose and Conjugate Transpose

Transpose and Conjugate Transpose are two important matrices that are widely used in mathematics. The difference between these two types of matrices is found in their operation. The transpose of a matrix is obtained by interchanging the rows and columns of that matrix. While the conjugate transpose is obtained by first taking the transpose of that matrix and then obtaining the complex conjugate of all the elements. The complex conjugate of a matrix is obtained by negating the imaginary parts of every element. Another important difference is that while taking conjugate transpose, the elements of the matrix under consideration are represented with their real as well as their imaginary parts. This is not the case while taking simple transpose of a matrix. In addition to this, there are two operations performed on the matrix in order to obtain its complex conjugate while in case of obtaining the transpose only one operation is performed.
Instructions
-
1
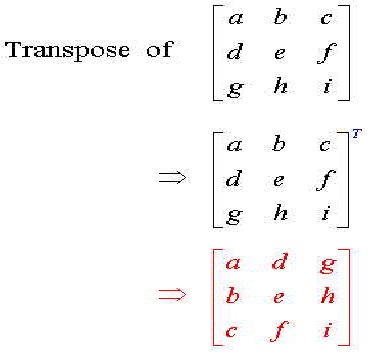
Transpose Matrix:
The transpose of matrix X is defined as the matrix X^T such that the columns are interchanged with the rows and vice versa. The resulting matrix also changes its size if the matrix X is mxn then the transpose matrix X^T changes into nxm.
Image Courtesy: evl.uic.edu
-
2
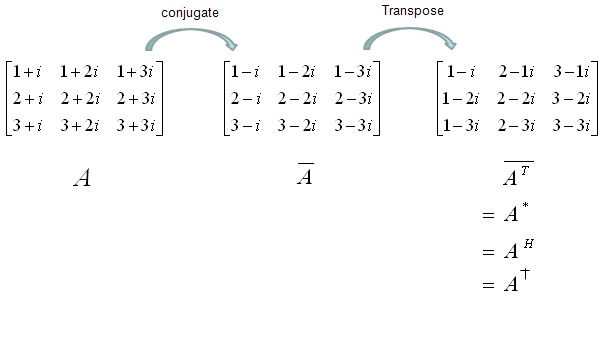
Conjugate Transpose:
The conjugate of matrix A is defined as matrix A such that A*=Ā^T. First the row elements of the matrix are changed with the elements of the columns and then the imaginary parts of every element is changed into negation.
Hermitian transpose and Hermitian conjugate are other names of conjugate transpose.
Image Courtesy: sharetechnote.com