Difference between Transpose and Inverse Matrix

In matrix algebra we often come across the basic linear transformations which are transpose and inverse matrices.
Both of these matrices are entirely different from each other.The major differences between the transpose and the inverse matrix exist in the matrices on which they are applied, the way they are found out and their results.
You may find out the transpose of any type of matrix but the inverse of a matrix is only applied on the square matrix. In addition to this, a matrix to be inverted must fulfil a necessary and sufficient condition which is that it must not be zero.
Another major distinction between the two is the way these are found out. In order to get the transpose of a matrix we have to simply rearrange the columns and rows of that matrix. On the other hand, there are several methods of obtaining the inverse of a matrix including block inversion, Gaussian elimination, Neuman series, Carmer’s rule, Eigendecomposition and Cholesky decomposition.
In addition to this, there also exists a difference in obtaining the results of these matrices. While obtaining the transpose of a matrix, we are not changing the values of the elements and only their position is being changed. On the other hand, the values of the resultant elements are altered when the inverse of a matrix is taken.
Also, the size of the matrix changes while taking the transpose of a matrix but the size does not change while taking an inverse of a matrix.
Instructions
-
1
Transpose:
It is defined as the matrix that is obtained by interchanging rows with columns or columns with rows. This will not only change the size of the matrix but also the indices of every element. However, the indices of the diagonal elements remain the same.
- Image Courtesy: katjaas.nl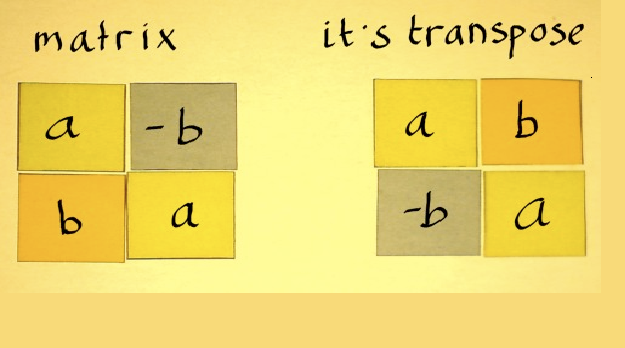
-
2
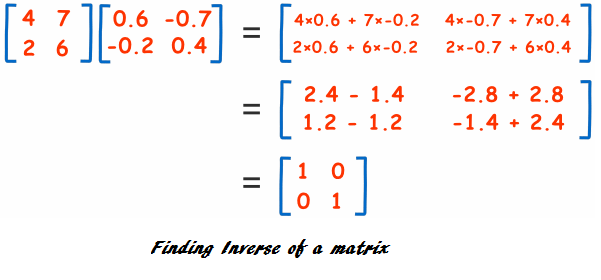
Inverse:
A matrix ‘X’ is said to be an inverse matrix if there is another matrix ‘Y’ such that it satisfies this equation: XY=YX=I. X will be called the inverse matrix of Y and Y will be called the inverse matrix of X. In addition to this there is a necessary and sufficient condition that matrix X must satisfy in order to be invertible. This necessary and sufficient condition is that the determinant of matrix X must be non zero.
- Image Courtesy: mathsisfun.com