How to Find the Area of a Circle Using Radius
Geometrical calculations are inevitable in a number of different aspects of daily life. Almost all the structures that are built around the world rely in one way or another on such calculations. If you find yourself in need of finding the total area of a perfect circle, rest assured that the task is very simple as long as you know the circle’s radius. All you will need to do would be to square the circle’s radius and then multiply it with π which equals 3.1416. This means that the mathematical formula for finding the area of a circle is πr2.
Things Required:
– Calculator
Instructions
-
1
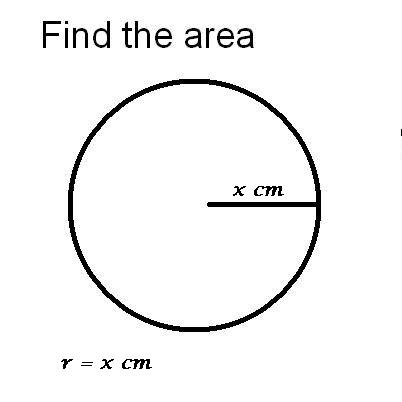
Determine the circle’s radius if you do not already know it. The radius of a circle can be defined as the distance between the centre of the circle and a point lying on the boundary of the circle. Consider the circle’s radius to be r.
-
2
In order to determine the radius, you will have to determine the circle’s diameter. This can be accomplished by drawing a perfect square in the circle in such a way that the four corners of the circle are in contact with the boundary of the circle. The circle’s diameter would be equal to the length of a diagonal running from corner of the square to its opposite corner. Divide the diameter by 2 and you will have the circle’s radius.
-
3
Square the radius (r) you determined in the previous step. For instance, if the circle’s radius was 7cm, square of the radius would be 49cm².
-
4
Finally, determine the circle’s area by multiplying result from the previous step with π (pi). The value of π is 3.1416 or 22/7. Using r² = 49 and π = 22/7, area A of the circle can be determined as follows.
A = πr²
A = π (49cm²)
A = 3.1416 × 49cm² = 153.93cm² = 154cm²