Difference between Integration and Summation
Integration and summation are the two concepts you should understand if you are studying mathematics or engineering related subjects. Both integration and summation are widely used in the engineering industry to solve complex problems. The concepts of integration and summation are also taught in high school mathematics. The use of these theories depends on the situation but it will not be fair to say that they share a very close relationship. Summation operation is performed where is a need to add a sequence of numbers and it is denoted by the letter of capital sigma. Integration on the other hand is known as the reverse operation of differentiation. In mathematics, it is also known as the area enclosed by the curve of the axis and the function.
Instructions
-
1
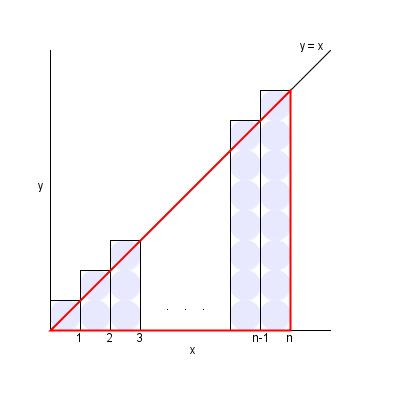
Summation
The letter sigma represents the sum or total of a numerical sequence. Recently, mathematicians have started to use the summation letter sigma to show how infinite sequences are added up. Furthermore, the summation process can also be used to represent the sum or total or matrices, polynomials and vectors. The summation operation is performed for a range of values or numbers to come up with a general term. The upper bound and the lower bound are the names given to the ending point and the starting point of the summation procedure.
In the example given below,
The sum of the sequence a1, a2, a3, a4, …, an is a1 + a2 + a3 + … + an which can be easily represented using the summation notation as ∑ni=1 ai, where i is the index of summation.
Depending on the application, the mathematician may choose to use variation for summation. For example, the summation process might use a defined set of numbers, denoted by the letter P. It is also possible to use more than one sigma sign depending on the requirements of the summation process. Consider learning the basics of algebra to better understand when and how the summation operation is applied.
- Image courtesy: elegantcoding.com
-
2
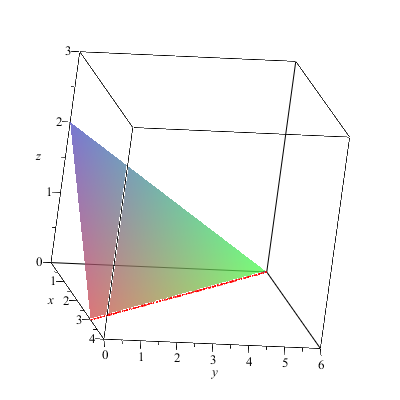
Integration
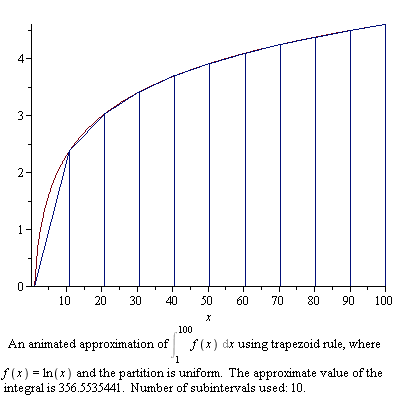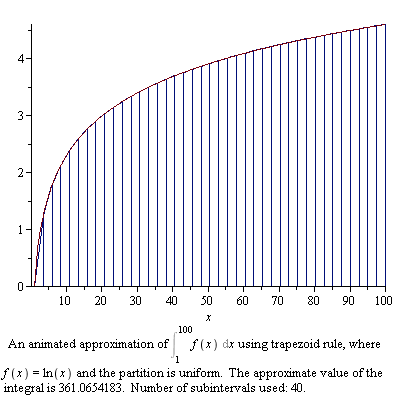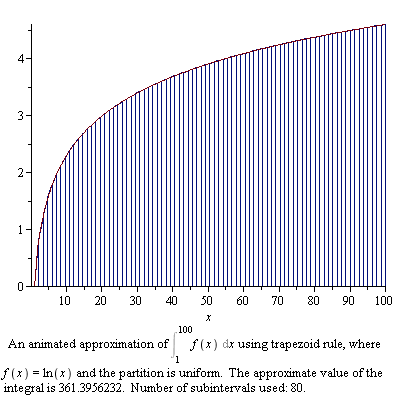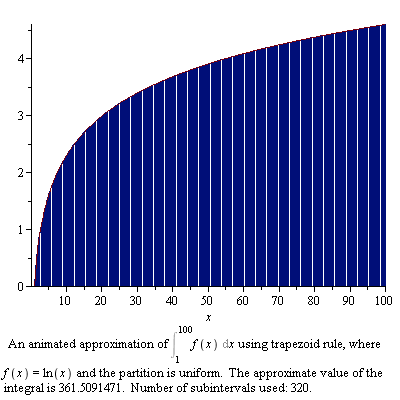
As discussed previously, the area enclosed by the curve or any geometrical figure is termed as the integration phenomenon. A complex equation solution should be performed to determine the area inside the curve. It is recommended to break the area into small pieces. Computing the area of these small pieces then determines the overall area under the curve. The integration operation is usually denoted by the Greek letter Pi.
- Image courtesy: maplesoft.com