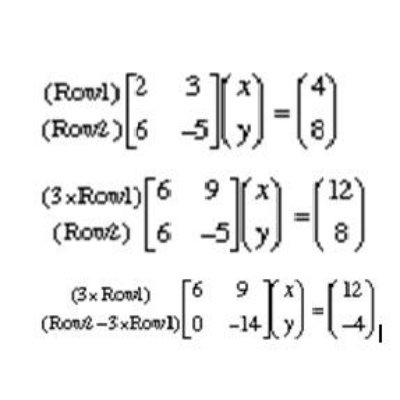How to Solve Simultaneous Equations Using Matrices

In some mathematical problems, we sometimes have to find 2 unknown values by solving 2 equations at the same time. Hence if are able to find one quantity, then it is easy to find the other one. For example, if there are 20 boys and girls together in a class and their exact number is unknown; this can easily be calculated if we know either number of boys or number of girls in that class. However, if we do not know either of the two numbers and for instance just know how many more or less boys than girls are there in a class, we can find both the numbers with the help of Simultaneous Equations. Therefore, two equations in which there are two unknowns are called Simultaneous Equations. Apart from the conventional method of solving Simultaneous Equations, they can also be solved with the help of Matrices quite easily.
Instructions
-
1
Normal Method of Solving Simultaneous Equations
For those who are new to Simultaneous Equations, there is a simple way of solving them. This is also called Elimination Method because it involves getting rid of one variable or unknown at one time. Look at the below given example:
Find the values of X and Y from the following two equations:
2x + y = 7 _______________________ Equation 1
3x - y = 8 ________________________ Equation 2
Adding Equation 1 & 2 we get:
2x + y = 7
3x - y = 8
--------------
5x = 15
x = 3
Now putting x = 3 in either equation 1 (or equation 2) we get:
2x + y = 7
2(3) + y = 7
6 + y = 7
Y = 7 – 6
Y = 1
Hence the required values are:
X = 3 and Y = 1 -
2
Word Problems involving simultaneous equations
The students of GCE, IGCS and Ordinary Level normally have to solve Word Problems that involve Simultaneous Equations. This may involve some trick but the students should not get confused with the wordings. Consider the following example:
Peter has more money than Bill. If Peter gives $20 to Bill, they will have the same amount. On the other hand if Bill gives Peter $22, then Peter would have twice as much as Bill. How much does each one actually have?
Solution. Let ‘x’ be the amount of money that Peter has and ‘y’ be the amount that Bill has.
(Note: Always use ‘x’ and ‘y’ for the symbolic representation of the unknown factors and make sure you know what they represent.)
As there are two unknowns so there will be two equations, because the number of equations must be equal to the number of unknowns. In order get two equations out of the given information, we translate each verbal sentence into algebraic language.
First sentence:
"If Peter gives Bill $20, they would have the same amount."
Algebraically:
X − 20 = Y + 20 ________________ Equation (1)
(Peter -- x -- has the same amount as Bill, after he gives him $20.)
Second sentence:
“If Bill gives Peter $22, then Peter would have twice as much as Bill."
Algebraically:
X + 22 = 2 (Y − 22) ______________ Equation (2)
(Peter has twice as much as Bill after Bill gives him $22.)
To solve any system of two equations, we must reduce it to one equation in one of the unknowns. In this example, we can solve equation (1) for x such as:
X − 20 = Y + 20
Implies that:
X = y + 40 ------------------- Equation (3)
Substituting value of ‘X’ it into equation (2):
X + 22 = 2 (Y − 22)
Y + 40 + 22 = 2(y − 22)
That is,
Y + 62 = 2y − 44,
Y − 2y = − 44 − 62
−Y= −106
Y = 106
Hence Bill has $106. Now putting value of Y in Equation (3) we get:
106 + 40 = 146
i.e. Peter has $146 -
3
Solving Simultaneous Equations using Matrices
If you want to avoid a long solution to find the unknown values in simultaneous equations then you can simply use Matrices as an alternative method. This can help you find the unknown values in quick time provided you know how to solve matrices and the row operation involved. Consider the following two equations:
2x + 3y = 4
6x – 5y = 8
The two equations can be represented in a single matrix equation as shown:
The matrix equation only involves the coefficients of x and y. As we used to eliminate an unknown value by adding or subtracting two equations, here we will need to use row operations to try to get zero's in that first matrix. We do this by multiplying the first row by some number so that we get the first element to be the same in both rows as shown in image:
We get the above after multiplying the first row by ‘3’ and now we have "6" as the first element in both rows. So we can now subtract that first row from the second row and we get:
In the above equation, we can see that there is only one non-zero element in the second row which is -14. Now when we again turn this back into equations, we can use that later equation and get the value of y as:
Y = -4/-14 or Y = 2/7
Putting Y = 2/7 in 2x + 3y = 4 and solving we get:
X = 11/7