Difference between Definite and Indefinite Integrals
If you are looking to learn the differences between indefinite and definite integrals, you will be glad to know that you have come to the right place. Calculus and algebra has numerous applications in mathematics as indefinite and definite integrals are the key to numerous problems in this field of work. The reverse process of differentiation is known as the integration.
When solving an integration problem, the solution provides an integral. Depending on the results given by the solution, the integral may be indefinite or definite. Indefinite integrals results in a family of functions giving indefinite whereas definite integrals produce definite solution with finite numbers.
Instructions
-
1
Indefinite Integrals
It will not be wrong to say that indefinite integral is a more generalised form of integration. For any given function, an indefinite integral acts as the anti derivative. If f is the integration of a function f then f will give an integral which can be written as follows:
F(x)=∫ƒ(x)dx or F=∫ƒ dx
Where both F and ƒ are functions of x
F is differentiable
The indefinite integral in the above function is also known as the Reimann integral. The resulting functions give an arbitrary constant. The name indefinite integral is given because it produces a set of functions, which result in indefinite integral. Using the concept of integration and indefinite integrals, a variety of integration and mathematical problems can be solved.
However, one has to learn the art of solving integration equations to find the indefinite integral. It should be noted that while differentiation follows simple rules and techniques, there is no clear standard method for integration. Solution of some integration problems cannot be expressed in simple terms of elementary functions. If this is the case then the resulting solution will be analytic in nature.
- Image Courtesy: vln.school.nz

-
2
Definite integral
As discussed before, integration equation containing definite integrals can be solved easily when compared to indefinite integral problems. Essentially, definite integrals are the counterpart of indefinite integrals and the actual integration process results in a finite number.
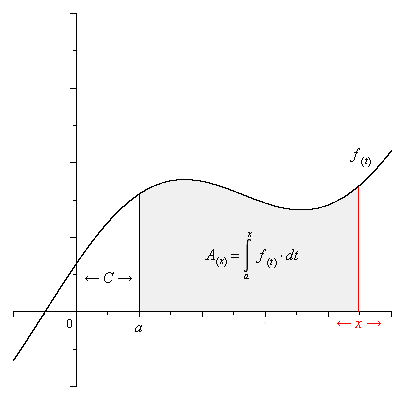
The definite integral can also be defined as the area under the curve for any function f with a provided interval.
When the integration process is applied on such a function, it produces a definite value which can be written as:
a∫bƒ(x)dx or a∫b ƒdx.
- Image Courtesy: mathnotes.org