Difference between Variance and Covariance
Variance and covariance are two statistical terms that are often confused by people. Considering the names of these two terms, students often think that they are difficult to separate; however, they are actually two distinct concepts. Variance is the measure of the scatter of the data, whereas covariance is defined as the measure of variation of two random variables, or the strength of correlation between those variables.
Covariance is a broader term as compared to variance, and the latter can be considered a special case of the former. Variance is an intuitive concept, whereas covariance is not that intuitive, and is always defined mathematically.
Both variance and covariance depend on the magnitude of the values in the given data, and cannot be compared and contrasted; this is the reason why their values can be easily normalized. Variance is normalized into standard deviation, while covariance is normalized into the correlation coefficient. Variance is normalized into standard deviation by taking its square root, whereas covariance is normalized by dividing each value of covariance by standard deviation.
Instructions
-
1
Variance
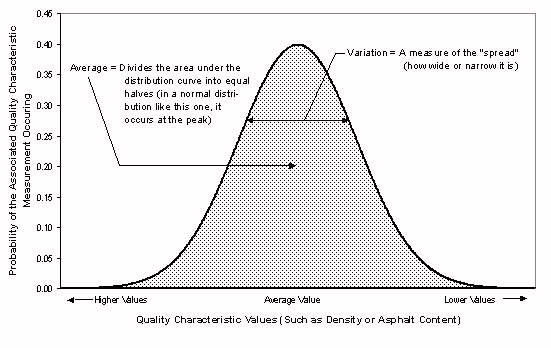
Variance, in statistics and probability theory, is defined as the measure of the dispersion of the statistical data from the mean value of the probability distribution. A probability distribution has various descriptors and variance is one of them, used to determine how far a set of numbers lies from the mean (expected value) of the distribution. It is also one of the several moments of the probability distribution, meaning that it can help distinguish between various probability distributions.
Furthermore, it is also a parameter of the population, meaning that it determines the actual probability distribution of a given population, and if the population is not fully observed, it can still be used to determine the theoretical probability distribution of a sample. If the standard deviation of a sample or population is given, its variance can be calculated by squaring the standard deviation.
The following formula is used to calculate variance.
For a population: Var(X)=E[(X-µ)2 ], and
For a sample: Var(X)=E[(X-‾x)2 ]
Image courtesy: classes.engr.oregonstate.edu
-
2
Covariance
Covariance, in statistical theory, indicates the degree of change of two random variables together; in other words, it is the measure of correlation between two random variables. When both random variables change proportionally, in the same direction, the covariance is positive, and vice versa.
The covariance between two random variables X and Y, with finite second momentum, is given by
σ(X,Y) = E [(X-E[X])(Y-E[Y])]
Image courtesy: beyondtheblueeventhorizon.blogspot.com