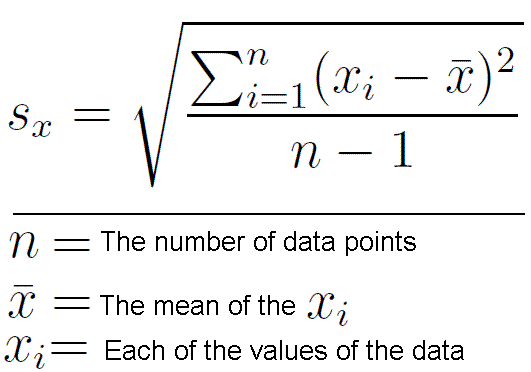Difference Between Variance and Standard Deviation
Dispersion refers to the absolute parameters of variation. It represents the mean square deviations of the various values of the trait from its average value. Is used to denote the sign σ ^ 2.
In probability theory, variance is a measure of the dispersion of a random variable that is a measure of its deviations from expectation. Also, directly from the dispersion is the definition of standard deviation.
In the theory of probability, it is a measure of the dispersion spread by a random variable that is a measure of its deviations from expectation.
Instructions
-
1
Variance:
The variance of the random variable X is the mean square deviation of a random variable from its mathematical expectation. The dispersion of a random variable can be expressed through a standard (rms) deviation of a random variable. The standard deviation of a random variable X is called square root of the variance of this magnitude: σ = sqrt (D [X]). The variance in mathematical statistics and probability theory is defined as a measure of dispersion (deviations from the mean).The smaller the value of this ratio, the more homogeneous population and those at closer range will be the average value. With this rule, you can determine how much of the total variance is affected by trait factor that underlies group. The higher the proportion of the between-group variance in general, the stronger will be the influence of this factor.
Image courtesy: learning.mazoo.net
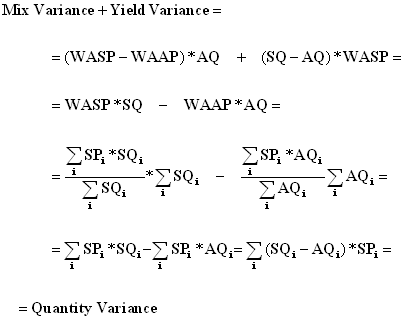
-
2
Standard deviation:
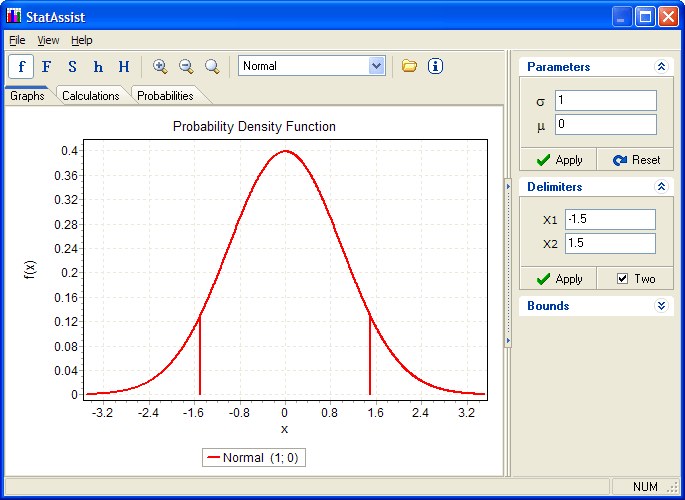
The standard deviation is an important quantitative characteristic of the statistics, probability theory and evaluation of measurement accuracy. According to the definition, standard deviation is called the square root of the variance. However, this definition is not quite clear - that characterizes this value and how to calculate the variance. Let there be a few numbers that characterize any similar quantities. For example, the results from weighing, statistical surveys, etc. All the values must be measured on the same unit of measurement. To find the root mean square deviation , determine the arithmetic average of all the numbers: add up all the numbers and divide the sum by the total number of numbers. Find the deviation of each number from its mean value: Subtract each number from the arithmetic mean. Determine the variance (range) numbers: Add the squares of deviations found earlier, and divide the sum by the number of numbers. Remove the square root of the variance. The resulting number is the standard deviation of a given set of numbers.
Image courtesy: statistics.about.com