How to Solve Exponential Equations using Logarithms
If you know how to solve algebraic expressions as well as indices, you should not be having much problem in solving exponential equations using logarithms. For example if there is an equation of the type 2x = 32, it can easily be solved by applying the laws of indices. All that is to be done in this equation is equating the bases of both sides. Considering it is 2x on the left side, you can make 25 on the right side. Since the bases will be equal, so the answer is simply x = 5. However, if there is an equation of the form 2x = 30 then you cannot go with the same method as the bases cannot be equalized. To solve such exponential equations, you have to apply Laws of Logarithms which are very easy to understand and apply.
Laws of Logarithms
– ln(xy) = ln(x) + ln(y)
– ln(x/y) = ln(x) – ln(y)
– ln(x r ) = r ln(x) for any real number ‘r’
Instructions
-
1
Getting Started
Before you go on to apply the Laws of Logarithms on a particular equation, confirm that it is of the type as given below:
ex = 80 -
2
Applying the appropriate law
The equation above suggests that you will have to apply one of the above three listed laws of logarithm. If you compare all three, it will be the third one which will solve the equation.
-
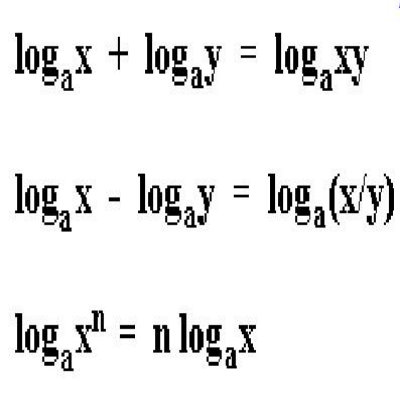
3
The Solution after applying law
Once you apply the law ln(x r ) = r ln(x) on ex = 80, you are actually taking log or ln on both sides of the equation.
Ln (ex ) = Ln (80)
X Ln (e) = Ln (80)
Since Ln (e) is equal to 1 so we write:
X = Ln (80)
As we look at the table of Logarithms for Ln (80), the value will be:
X = 4.38202663467
This means:
e4.38202663467 = 80
 = ln(x) + ln(y)
- ln(x/y) = ln(x) – ln(y)
- ln(x r ) = r ln(x) for any real number 'r'Next%20stop%3A%20Pinterest "Pin It")
