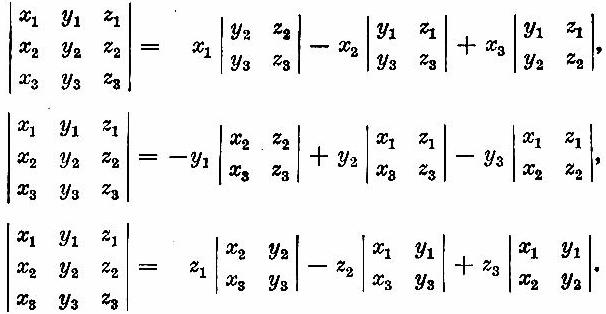Difference between Matrix and Determinant

Matrices and determinants are two of the most important concepts when it comes to linear algebra. Both are mathematical forms of representing various mathematical parameters and have clear differences between them.
A matrix normally represents a group of number, which further represent an equation. The determinant, on the other hand, is just a number, which can also represent the volume. A determinant is the product of a matrix and can only be obtained from square ones.
There is a difference in the way mathematical operations are carried out for matrices and determinants. A determinant is just a number and it can be multiplied, divided, added, or subtracted to a matrix or any other number normally. To carry out algebraic operations between two or more matrices, there are a special set of rules. In addition to that, the inverse of a matrix cannot be calculated if there isn’t a determinant.
Instructions
-
1
Matrix
Matrix is a rectangular array of numbers which are arranged in the forms of rows and columns. The size and the mathematical operations of the matrix depend on the number of rows and columns. If the number of rows within a matrix is same as the number of columns in it, the matrix is referred to as the square matrix.
There are many types of matrices. A matrix with a single column is called a vector, one with a single row is called a row matrix and one with only zeroes in it is called a zero matrix.
There are many other criterions on the basis of which the matrices are defined. The most notable parameter in this regard is the diagonal of the matrix and the elements in, above and below it.
Matrices can be used in solving linear algebraic equations in a quick way. Their logic is used many computational programs to save the calculation time and the storage space; it is therefore a fundamental tool of finite element analysis.
Image courtesy: coburgmathsmethods12.pbworks.com

-
2
Determinant
A determinant is a number which is obtained by carrying out certain defined mathematical operations inside a square matrix. This method is different for square matrices of different sizes.
Determinant is mandatory in calculating the inverse of a matrix. This number is not inconsequential or only a calculation tool. It has his physical application in liner algebra as well. This number represents the volume of a square area.
Image courtesy: mpec.sc.mahidol.ac.th